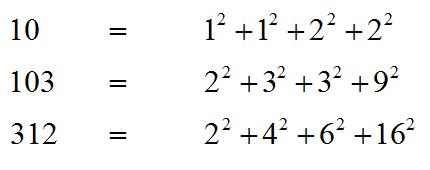Euler Four-Square Identity -- from Wolfram MathWorld

The amazing polynomial identity communicated by Euler in a letter to Goldbach on April 12, 1749 (incorrectly given as April 15, 1705--before Euler was born--in Conway and Guy 1996, p. 232). The identity also follows from the fact that the norm of the product of two quaternions is the product of the norms (Conway and Guy 1996).

What is the value of n, if 1 - 1/2 + 1/3 - 1/4 + … - 1/2012 + 1

Special Functions in Wolfram, Alpha—Wolfram

Colloquium - WCU of PA

Predicting the Structures of Glycans, Glycoproteins, and Their

Numerical nonlinear frequency analysis of pre-damaged curved

Bruce F.Torrence, Eve A.Torrence - The Student's Introduction To

Elementary Number Theory - Linköping University

These two equations are equivalent but Desmos and Geogrbra both

Processing benfry part 2 by Byron Sin - Issuu

Euler's Four-square Identity

Open problem in number theory

The Most Striking Equation in Mathematics – Galileo's Pendulum

From Euler's equation we can find that, e^(2π) = (1) ^(- i) But

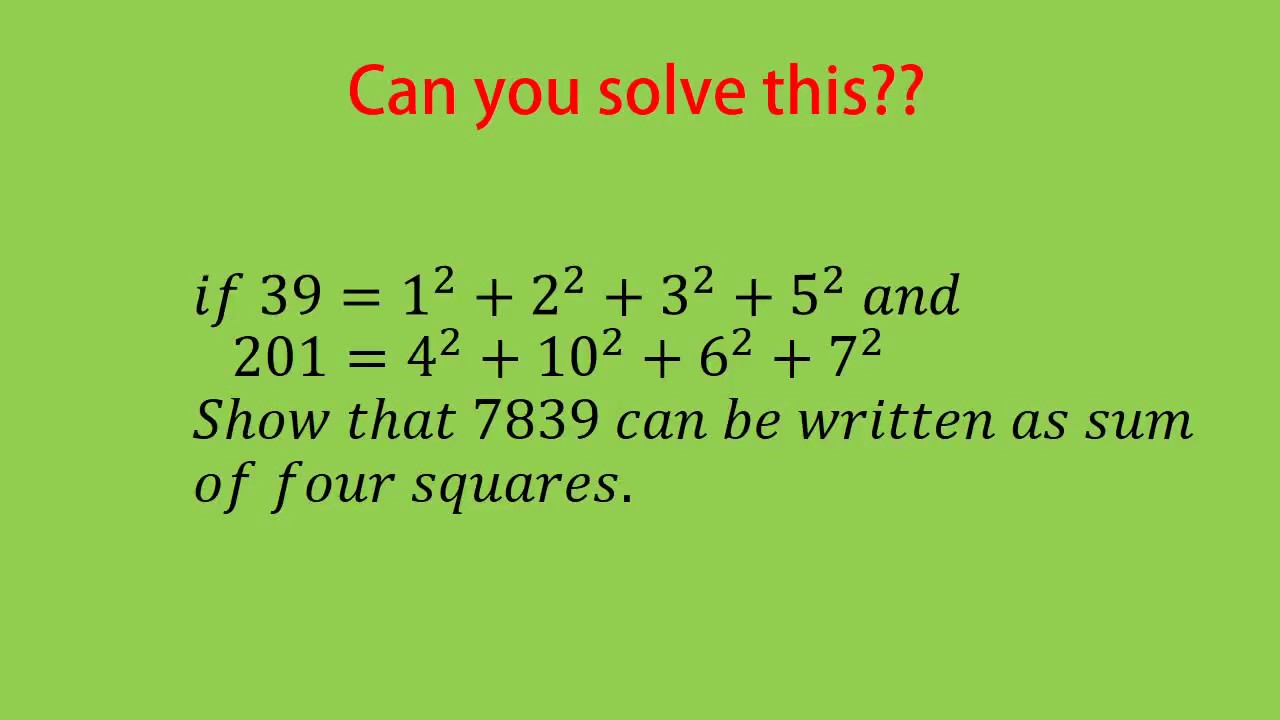
Sum of four Squares

Maths Ed Ideas: On π